
 |
|
|
Регистрация Восстановить пароль |
|||||||
| Регистрация | Задать вопрос |
Заплачу за решение |
Новые сообщения |
Сообщения за день |
Расширенный поиск |
Правила |
Всё прочитано |
||||
 |
|
|
|
Опции темы | Поиск в этой теме |
|
|
#1 | |||
|
Пользователь
Регистрация: 19.08.2013
Сообщений: 11
|
Паттерн
В 2002 году придумал интересную штуку. 14 лет тогда было. Размышлял о фракталах и теории хаоса, а учиться не хотел. Учиться не хотел, а в школу ходить заставляли. Придумал способ убить время на скучных уроках по истории, географии и прочей гуманитарии. Попробую объяснить подробно. Все, что нам нужно - листок в клетку и карандашик. Если листка в клетку нет в наличии и карандашик тоже отсутствует - онлайн версия на JavaScript http://xcont.com/pattern.html (в исходники не заглядывайте - тем говнокод Алгоритм прост до неприличия. Собственно выглядит сие вот так: 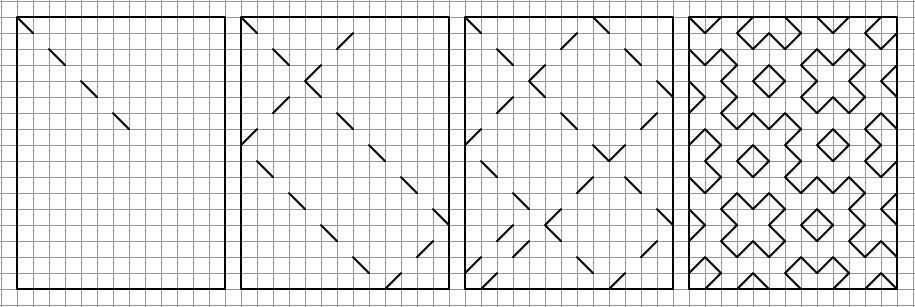 Выделяем прямоугольную область и пускаем из угла "квантовый луч" (так я его называл в 2002 году - сильно за терминологию не ругайте). Луч отражается от стенок и пропадает в другом углу. Если соблюдаются определенные условия (об этом дальше) - получается фрактальный (об этом тоже дальше) узор-паттерн. Если условия не соблюдаются (очевидный например - стороны прямоугольника равны) - узор не получается. Из менее очевидных напримеров - узор так-же не получается, если размеры сторон имеют общий делитель. Фактически, узоры получаются только если размеры обоих сторон - взаимно простые числа (http://ru.wikipedia.org/wiki/Взаимно_простые_числа ). Наглядно (кликабельно):  кстати, все сделано вручную, по пикселям в Paint На картинке все числа от 1 до 30. А теперь немного о Фибоначчи и фракталах. Все узоры представляют из себя фракталы. От чего зависит узор? Цитата:
http://ru.wikipedia.org/wiki/Числа_Фибоначчи Закрашивал в Paint самые большие замкнутые области. 233х144:   987х610 (скукожил в 5 раз):  233х144 и 987х610 - идентичны  Фракталы, как они есть. Что еще можно из этого сделать: 1. Попробовать не прямоугольную область, а скажем элипс. 2. Попробовать сделать в трех измерениях. 3. Обнаружить другие интересные зависимости между числами и рождаемым ими фракталом. На хабре объяснил не подробно, о чем сейчас жалею. http://habrahabr.ru/sandbox/68846/ Есть интересная информация, чтобы дополнить статью, но дополнить не могу - ибо read-only. Поэтому буду выпрашивать инвайт, если кому не жалко (пазязя) Засим откланяюсь и буду надеяться на вашу доброту (дайти инвайтик, пазязя). Инвайтик сюда: admin@xcont.com или сюда: serg530@i.com.ua P.S. И немножко шизофрении 11-ти летней давности: Цитата:
Цитата:
|
|||
|
|

|
|
|
#2 |
|
Форумчанин
Регистрация: 30.05.2011
Сообщений: 651
|
Скажи, а чё ты куришь? )))
Создание, программирование и сопровождение сайтов любой сложности.
Изготовление программ на заказ. Список услуг и портфолио на сайте www.andreygrom.ru |
|
|

|
|
|
#3 |
|
Linux C++ Qt ARM
Старожил
Регистрация: 30.11.2008
Сообщений: 3,030
|
Ничего не понял, но картинки красивые.
Дилетант широкого профиля.
"Слова ничего не стоят - покажите мне код!" © Линус Торвальдс |
|
|

|
|
|
#4 | |||
|
Старожил
Регистрация: 30.12.2009
Сообщений: 11,434
|
Цитата:
Цитата:
Не соблюдается одно простое условие: Каждый следующий фрагмент изображения, подобен всей фигуре в целом и является её неотъемлемой частью. Вот вам пример фрактала: И да: Цитата:
Последний раз редактировалось Человек_Борща; 20.08.2013 в 08:52. |
|||
|
|

|
|
|
#5 |
|
Участник клуба
Регистрация: 11.08.2012
Сообщений: 1,226
|
На фрактал не похоже. Но что-то в этом есть красивое.
|
|
|

|
|
|
#6 | ||
|
Пользователь
Регистрация: 19.08.2013
Сообщений: 11
|
Цитата:
Цитата:

|
||
|
|

|
|
|
#7 |
|
Форумчанин
Регистрация: 30.05.2011
Сообщений: 651
|
Пытливый склад ума - это хорошо. Было бы ещё лучше, если бы этот "календарь Майя" на практике бы кому пригодился...
Создание, программирование и сопровождение сайтов любой сложности.
Изготовление программ на заказ. Список услуг и портфолио на сайте www.andreygrom.ru |
|
|

|
|
|
#8 |
|
Пользователь
Регистрация: 19.08.2013
Сообщений: 11
|
Спираль Улама - она ведь тоже абсолютно бесполезна. Кстати, эти фрактальчики вспомнил в 2011 году, когда простые числа обсуждали на одном форуме. Кто-то спираль Улама вспомнил, а я вот это.
На практике - можно ковры вышивать. 
|
|
|

|
|
|
#9 |
|
Старожил
Регистрация: 17.11.2010
Сообщений: 18,922
|
xcont, все правильно. Глядишь что-то и получится. Вдруг закон распределения простых чисел получишь, чем черт не шутит.
 А пока + А пока +
Если бы архитекторы строили здания так, как программисты пишут программы, то первый залетевший дятел разрушил бы цивилизацию
|
|
|

|
|
|
#10 |
|
я получил эту роль
Старожил
Регистрация: 25.05.2007
Сообщений: 3,694
|
Забавно, жаль на хабре не заметили. Пилите теперь визуализацию с наворотами
 Первое, что приходит в голову, — сделать "луч" не просто пунктиром, а заранее заданным паттерном, или простыми числами (два тире, три пробела, пять тире, семь пробелов...) Первое, что приходит в голову, — сделать "луч" не просто пунктиром, а заранее заданным паттерном, или простыми числами (два тире, три пробела, пять тире, семь пробелов...)Вот, к слову, красивая визуализация отношений между натуральными и простыми числами http://www.jasondavies.com/primos/
пыщь
|
|
|

|
 |
|
 Похожие темы
Похожие темы
|
||||
| Тема | Автор | Раздел | Ответов | Последнее сообщение |
| Даны целые числа р и q. Получить все делители числа q, взаимно простые c г. | Владан | Паскаль, Turbo Pascal, PascalABC.NET | 2 | 03.12.2012 23:39 |
| Задачи в ТурбоПаскаль: найти числа Армстронга и просуммировать числа в последовательности номера которых простые числа | Lena1808 | Помощь студентам | 1 | 17.05.2012 08:00 |
| Взаимно простые числа | Bek-Z | Помощь студентам | 6 | 24.12.2010 20:57 |
| Даны взаимно простые натуральные числа m и n (m>n). Найти переодическую и непереодическую части десятично | Angel-dm | Паскаль, Turbo Pascal, PascalABC.NET | 0 | 27.04.2010 19:02 |